About FOPS

Search for the Best

Always try to find the best possibility from the set of available solutions. Using FOPS it is guaranteed that you can say: “I have tried to do my best!”

How many objectives?

User can choose one of currently available algorithms: GA, PSO, DE, SOMA, Nelder-Mead and Newton methods for single objective problems; NSGA-II, MOPSO and GDE3 methods for multi-objective problems; and modification of single-objective PSO algorithm for problems with variable number of dimensions. The package can be controlled through GUI or directly by low level functions. Results of simulation run can be easily visualized in MATLAB figures or exploited elsewhere.

Chain

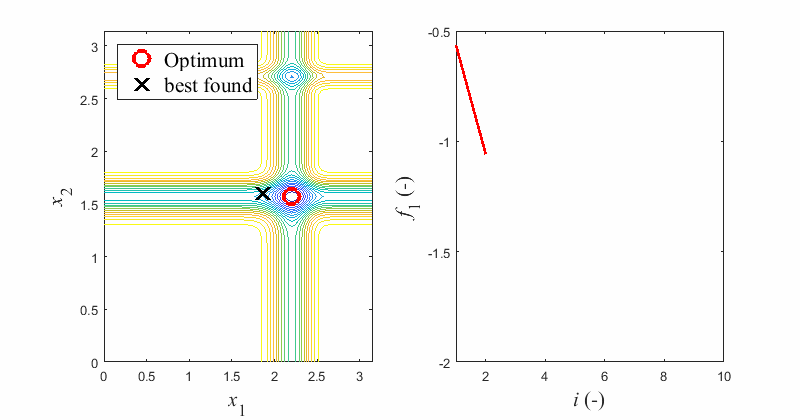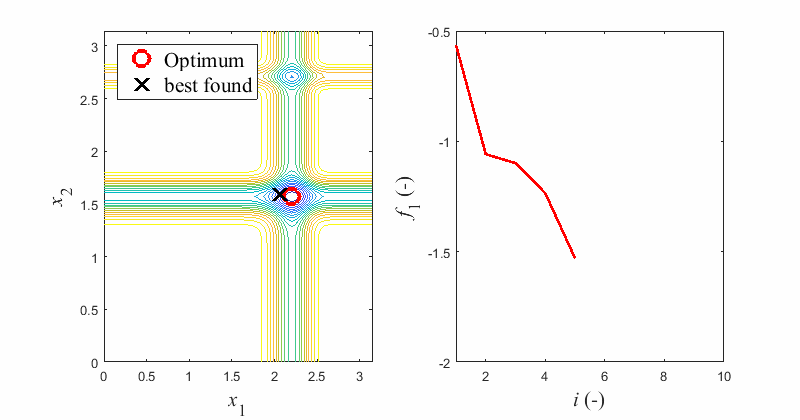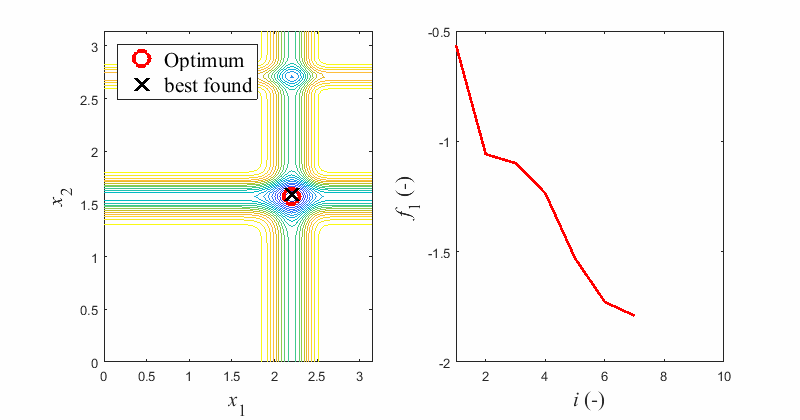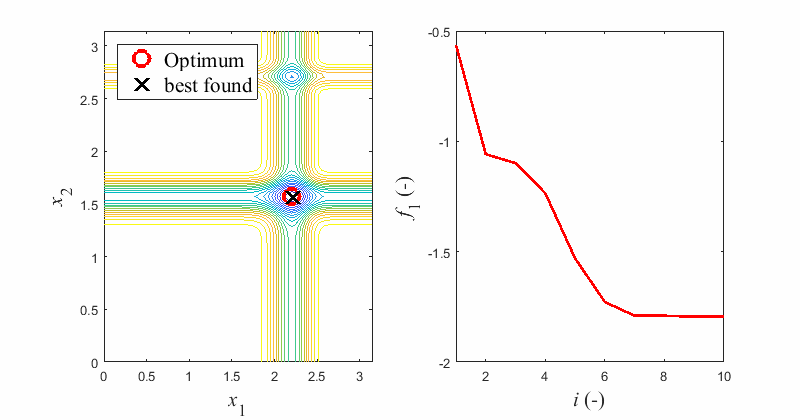
Some algorithms are good in exploration, while the others excel in exploitation. Therefore, user can take advantage of combining elementary optimization algorithms into chains to utilize their benefits. Chain of multiple constituent algorithms can be exploited on a single optimization problem. User can set the balance between usages of individual algorithms by setting their number of fitness function evaluations.

Comparative study

Comparative studies can be easily performed with FOPS toolbox and the performance of various optimization tasks or chains can be compared based on numerous predefined metrics. There are more than 50 multi-objective, single-objective and VND test problems but a user can define his own problems.

Discrete variables

In real life, some problems need to choose some variables in optimization task to be from a set of discrete values. In FOPS, every algorithm, either binary-coded or real-coded, can work with discrete decision space of optimized problem. User just provides list of discrete values for specified variable of the solved problem.

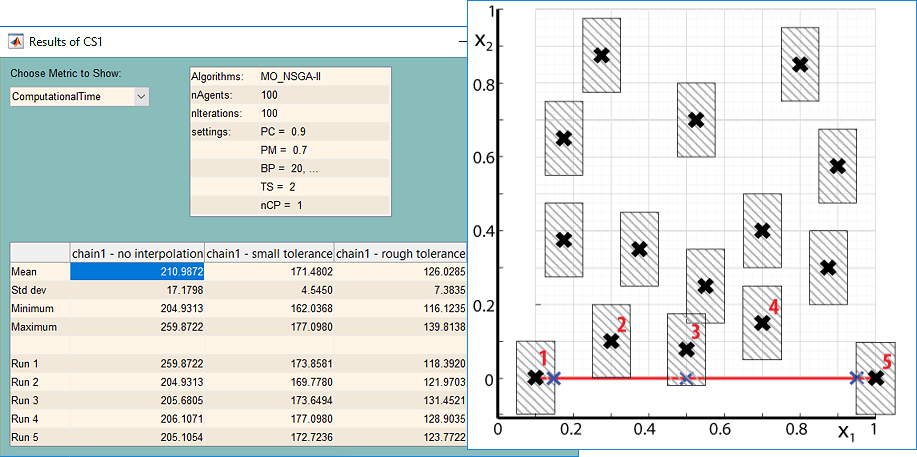
Interpolation

All algorithms can also exploit interpolation technique and save fitness function evaluations if they are costly. An improvement is obvious even when a fitness function evaluation takes 20ms. Imagine the difference with a real-world costly problems, where each evaluation takes 30 minutes or even more.

Variable dimensions

What is the ideal complexity of my design? Sometimes, sufficient complexity of optimized design is not known a priori. A VND (Variable Number of Dimensions) optimizer is able to work with different decision space sizes and find the ideal dimensionality and variables combination at one run [1]!

1. Kadlec, P., Sedenka V.: Particle swarm optimization for problems with variable number of dimensions, Engineering Optimization, Taylor & Francis, pp. 1-18, 2017.
2. Other are references in Documentation, see Download.